[BOJ/C++] 1463::1로 만들기 (DP)
1로 만들기
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
| 0.15 초 | 128 MB | 284044 | 96290 | 61385 | 32.823% |
문제
정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.
- X가 3으로 나누어 떨어지면, 3으로 나눈다.
- X가 2로 나누어 떨어지면, 2로 나눈다.
- 1을 뺀다.
정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.
입력
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
출력
첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.
예제 입력 1 복사
2
예제 출력 1 복사
1
예제 입력 2 복사
10
예제 출력 2 복사
3
힌트
10의 경우에 10 → 9 → 3 → 1 로 3번 만에 만들 수 있다.
후기
DP문제는 여전히 많이 어려운 것 같다. 이번 문제는 다른분들의 풀이를 참고했다.
이번 문제는 주어진 숫자를 최소한의 연산으로 1로 만드는 문제이다.
이 문제의 조건은 3가지이다.
- 3으로 나누어 나머지가 0이라면, 3으로 나눌 수 있다.
- 2로 나누어 나머지가 0이라면, 2로 나눌 수 있다.
- 1을 뺄 수 있다.
위 조건을 토대로 처음에는 탑-다운으로 접근할까 했지만, 연산과정이 DFS가 되어버려 과부화가 올것 같았다.
다른 풀이방법으로는 바텀-업으로 진행하며, 연산된 값을 토대로 다음 연산을 하는 것이 아닌 1~N까지 모든 수가 각 연산과 어떤 관계인지를 확인하는 방법(순차탐색O(n))이었다.
이를 설명하자면, 10이라는 값이 주어졌을때, 다음과 같은 일이 일어난다.
- 0번째, 자리는 배열을 사용하는 연산의 편의를 위해 비워둔다.
- 배열의 자릿수(크기)는 1~N을 표현하고, 각 배열 원소는 해당 자릿수가 될 수 있는 최소 연산 값을 넣는다.

| 2에서 1이될 수 있는 연산 찾고 연산 횟수가 더 적은 것을 배열[2]에 넣는다. | |||||
| 자릿수 | 목표 숫자 | 사용 가능 연산 | 조건 | 연산 | 연산 횟수 |
| 2 | 1 | +1 | 배열[1]의 최소 연산 횟수 + 1 = 1 | 1 | |
| / 2 | 2%2 == 0 | 배열[1]의 최소 연산 횟수 + 1 = 1 | 1 | ||
| /3 | 3%2 != 0 | 불가능 | |||
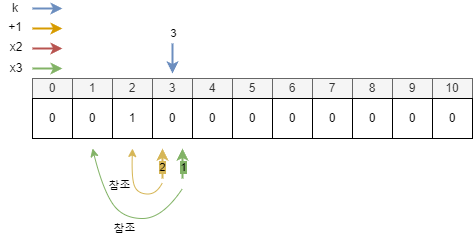
| 3에서 1이될 수 있는 연산 찾고 연산 횟수가 더 적은 것을 배열[3]에 넣는다. | |||||
| 자릿수 | 목표 숫자 | 사용 가능 연산 | 조건 | 연산 | 연산 횟수 |
| 3 | 1 | +1 | 배열[2]의 최소 연산 횟수 + 1 = 1 | 2 | |
| /2 | 3%2 != 0 | 불가능 | |||
| /3 | 3%3 == 0 | 배열[1]의 최소 연산 횟수 + 1 = 1 | 1 | ||
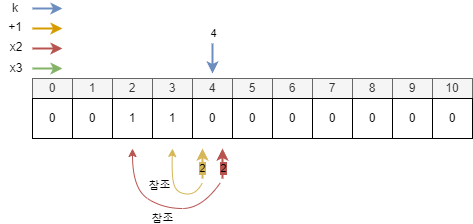
| 4에서 1이될 수 있는 연산 찾고 연산 횟수가 더 적은 것을 배열[4]에 넣는다. | |||||
| 자릿수 | 목표 숫자 | 사용 가능 연산 | 조건 | 연산 | 연산 횟수 |
| 4 | 1 | +1 | 배열[3]의 최소 연산 횟수 + 1 = 2 | 2 | |
| /2 | 4%2 == 0 | 배열[2]의 최소 연산 횟수 + 1 = 2 | 2 | ||
| /3 | 4%3 != 0 | 불가능 | |||
4부터 차이를 체감할 수 있다.
우선 +1연산은 배열[3]이 가지는 최소 연산 횟수에서 +1 연산을 추가한 것이기에 연산 횟수가 2가 된다. (배열[3]을 보는 이유는 +1연산으로 4가 될 수 있는 유일한 방법이며 3은 1회의 연산만으로 1이 될 수 있기에 최소 연산은 2회가 된다.
/2는 배열[2]의 최소 연산 수에서 1을 더해준다. (+1연산과 동일한 이유로 4를 2로 나눈 값 = 2를 1로 바꾸어주는 최소 연산 횟수는 이미 구해져 있기에, 해당 값에 1을 더하면 된다.)
그럼 모든 연산자가 포함되는 6을 한번 보자.
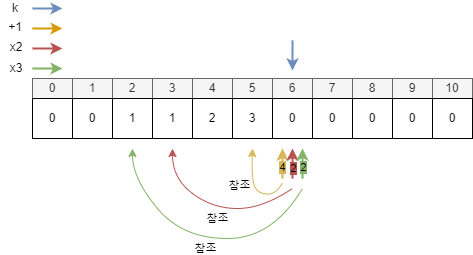
| 6에서 1이될 수 있는 연산 찾고 연산 횟수가 더 적은 것을 배열[6]에 넣는다. |
|||||
| 자릿수 | 시작 숫자 | 사용 가능 연산 | 조건 | 연산 | 연산 횟수 |
| 6 | 배열[5] | +1 | 배열[5]의 최소 연산 횟수 + 1 = 4 | 4 | |
| 배열[3] | /2 | 6%2 == 0 | 배열[3]의 최소 연산 횟수 + 1 = 2 | 2 | |
| 배열[2] | /3 | 6%3 == 0 | 배열[2]의 최소 연산 횟수 + 1 = 2 | 2 | |
이런 식으로 계산이 이어져 나아간다. 그림을 그리고 보니 개념 자체는 간단해 보인다.
코드
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(nullptr); cout.tie(nullptr);
int n;
cin >> n;
vector<int> storage(n + 1, 0);
for (int k = 2; k <= n; k++) {
storage[k] = storage[k - 1] + 1; // +1연산) 이전 위치와 현재 위치의 관계
if (k % 3 == 0) storage[k] = min(storage[k], storage[k / 3] + 1); // *3연산) (현재 위치/3) 자리 숫자와 현재 숫자의 관계
if (k % 2 == 0) storage[k] = min(storage[k], storage[k / 2] + 1); // *2연산) (현재 위치/2) 자리 숫자와 현재 숫자의 관계
}
cout << storage[n] << endl;
return 0;
}