티스토리 뷰
이번 장을 쓰면서 수식이용을 좀 용의하게 하기위해 HTML편집으로 스크립트를 넣었더니 임시저장했던 전에 작성했던 내용들이 다 사라졌다....
무튼 다시 쓰는겸 이전에 놓친 부분이 있나 생각하며 작성해보자.
이번 장은
벡터를 활용한 움직임 제어나 모델링 폴리곤의 사용되는 피타고라스의 정리,
충돌 검출 및 운동 법칙에 사용하는 거리 공식,
2차원과 3차원에서 움직일 때의 경로를 나타내는 포물선,
둥근 물체의 운동 경로 및 충돌 검을에 사용되는 원과 구 등
앞으로 등장할 전반적 모든 기하학 관련 주제 언급하는 장이다.
[피타고라스의 정리] : 두 점 사이의 거리
화면상 존재하는 두 오브젝트나 점 사이의 거리를 알아야하는 경우는 많다.
이때, 두 점 사이의 거리를 효율적으로 계산하는 것은 매우 중요한데 가장 간단하게 사용되는 방법이
피타고라스의 정리를 이용한 방법이다.
피타고라스의 정리는 모든 삼각형이 아닌 직삼각형에만 적용되는 정리이다.
피타고라스의 정리 공식
피타고라스의 정리는 가로, 세로, 빗면의 길이를 a, b, c라 가정한 직각삼각형에게 다음 공식이 성립된다.
$a^2 + b^2 = c^2$
$\sqrt{a^2 + b^2} = c$
$\sqrt{(a_2 - a_1) + (b_2 - b_1)} = c$
* 반대로 해당 공식이 성립하는 삼각형은 모두 직각삼각형이다.
3차원 거리의 거리 공식
$x^2 + y^2 + z^2 = c^2$
$\sqrt{x^2 + y^2 + z^2} = c$
$\sqrt{(x_2 - x_1) + (y_2 - y_1) + (z_2 = z_1)} = c$
--------------------------
2차원 거리의 공식가령 위와 같은 삼각형에서 세 점 A, B, C의 좌표를 다음처럼 설정할 수 있다.
A $(x_1, y_1)$, B $(x_2, y_2)$, C $(x_1, y_2)$
이러면 변 c의 길이를 피타고라스의 정리를 적용하여 다음처럼 적용이 가능하다.
$c^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$
$c = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
// 다양한 수식이 선언된 라이브러리 적용
#include <cmath>
// 함수 호출 스택을 거치지 않고 CPU의 FPU로 바로 수행하게 해주는 전처리기 명령어
#pragma intrinsic(sqrt, pow)
// 두 점 사이의 거리를 계산하는 함수
float Vector2_Distance(float *p1, float *p2)
{
// 두 점 사이의 거리 계산
return (float)sqrt(pow(p2[0] - p1[0], 2) + pow(p2[1] - p1[1], 2));
}<cmath>에는 제곱근, 제곱, 절대값, 삼각함수 등 다양한 수식을 제공하는 라이브러리이다.
이중 수를 받아 제곱근을 리턴하는 sqrt()함수나 받은 두번째 파라미터만큼 제곱을 해주는 pow()함수는 직접 곱하는 것보다 함수 호출을 위해 스택을 한번 거치기 때문에 느리다. (예, pow(2, 2)는 2 * 2보다 느리다.)
하지만 마이크로소프트 컴파일러를 사용한다면, #progma intrinsic 전처리기 명령어를 사용하여 이 단점을 크게 개선할 수 있다. 해당 명령어는 함수 호출을 스택을 거치지 않고 바로 CPU의 FPU에서 수행하도록 해준다.
또한 연산의 형변환으로 인한 결과 값의 변화를 막기위해 powf(), sqrtf()와 같은 자료형 전용 함수도 존재한다.
중점 공식
화면상의 두 물체 사이의 절반되는 위치를 정확하게 알 수 있는 공식이다.
두 점 : $P_1 (x_1, y_1), P_2 (x_2, y_2)$, 두 점의 중심 : $m$
$m(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2)}{2})$
#include <iostream>
using namespace std;
typedef struct Vector3{
float x, y, z;
Vector3(): x(0), y(0), z(0) {}
Vector3(float x, float y, float z): x(x), y(y), z(z) {}
} Vector3;
typedef struct Vector2{
float x, y;
Vector2(): x(0), y(0) {}
Vector2(float x, float y): x(x), y(y) {}
} Vector2;
Vector3 MidPoint(Vector3 _point1, Vector3 _point2);
Vector2 MidPoint(Vector2 _point1, Vector2 _point2);
int main()
{
Vector3 v3_1 = {10, 2, 5};
Vector3 v3_2 = {43, 21, 1};
Vector3 answer1 = Vector3();
Vector2 v2_1 = {3, 9};
Vector2 v2_2 = {21, 10};
Vector2 answer2 = Vector2();
answer1 = MidPoint(v3_1, v3_2);
answer2 = MidPoint(v2_1, v2_2);
cout << "Answer to Vector 3 : (" << answer1.x << ", " << answer1.y << ", " << answer1.z << ")" << endl;
cout << "Answer to Vector 2 : (" << answer2.x << ", " << answer2.y << ")" << endl;
return 0;
}
// 3차원 거리계산 함수는 z값까지 연산하도록 만들면 된다.
/// <summary>선분의 중점을 계산하는 함수</summary>
/// <param name="_point1">첫 번째 좌표</param>
/// <param name="_point2">두 번째 좌표</param>
/// <return>중점 위치 반환</return>
Vector3 MidPoint(Vector3 _point1, Vector3 _point2)
{
// 중점 좌표에 필요한 메모리 할당
Vector3 temp = Vector3();
// 중점 공식을 사용한 중점 계산
temp.x = ((_point1.x + _point2.x) / 2);
temp.y = ((_point1.y + _point2.y) / 2);
temp.z = ((_point1.z + _point2.z) / 2);
return temp;
}
Vector2 MidPoint(Vector2 _point1, Vector2 _point2)
{
// 중점 좌표에 필요한 메모리 할당
Vector2 temp = Vector2();
// 중점 공식을 사용한 중점 계산
temp.x = ((_point1.x + _point2.x) / 2);
temp.y = ((_point1.y + _point2.y) / 2);
return temp;
}
예제2.1 : 화면상 두 점 거리 찾기
점 (25, 80)과 (55, 40)사이의 거리를 구하라
$AB = \sqrt{(55 - 25)^2 + (40 - 80)^2}$
$\sqrt{(30)^2 + (-40)^2}$
$\sqrt{900 + 1600}$
$\sqrt{2500}$
$AB = 50$
예제2.2 : 직각삼각형 검사
A(20, 50), B(100, 90), C(70, 150) 세 꼭지점으로 이루어진 삼각형이 직각삼각형인가?
* 선 하나씩 전부 길이를 먼저 계산하면된다.
1. AB를 계산하기
$\sqrt{(100 - 20)^2 + (90 - 50)^2)} = \sqrt{(80)^2 + (40)^2} = \sqrt{6400 + 1600} = \sqrt{8000}$
2. BC를 계산하기
$\sqrt{(70 - 100)^2 + (150 - 90)^2)} = \sqrt{(-30)^2 + (60)^2} = \sqrt{900 + 3600} = \sqrt{4500}$
3. AC를 계산하기
$\sqrt{(70 - 20)^2 + (150 - 50)^2)} = \sqrt{(50)^2 + (100)^2} = \sqrt{2500 + 10000} = \sqrt{12500}$
이제 피타고라스의 정리를 이용하여 직각삼각형인지 판단한다.
$a^2 + b^2 = c^2$
$\sqrt{8000} + \sqrt{4500} = \sqrt{12500}$
정답 : 직각삼각형이 성립한다.
예제 2.3 : 3차원 상의 두 점 사이의 거리
좌표 (25, 80, 30), (55, 40, 100) 사이의 거리를 구하라
3차원의 거리 공식은 2차원에서 z축만 추가한 것이다.
$\sqrt{(55 - 25)^2 + (40 - 80)^2 + (100 - 30)^2}$
$= \sqrt{(30)^2 + (-40)^2 + (70)^2}$
$= \sqrt{900 + 1600 + 4900}$
$= \sqrt{7400}$
$= 86.02....$
예제 2.4 : 화면상의 두 점 사이의 중점
좌표 (25, 80), (55, 40)의 중점을 구하라
$ ((25 + 55)/2$, $(80 + 40)/2) $
$= (80/2, 120/2) = $
$= (40, 60)$
예제 2.5 : 3차원 상의 두 점 사이의 중점 구하기
좌표 (25, 80, 30), (55, 40, 100) 사이의 중점을 구하라
3차원의 거리 공식은 2차원에서 z축만 추가한 것이다.
$= ((25 + 55)/2$, $(80 + 40)/2$, $(30 + 100)/2)$
$= (80/2, 120/2, 130/2)$
$= (40, 60, 75)$
스스로 평가
1. 그림 2.4에서 변 b의 길이를 구하십시오
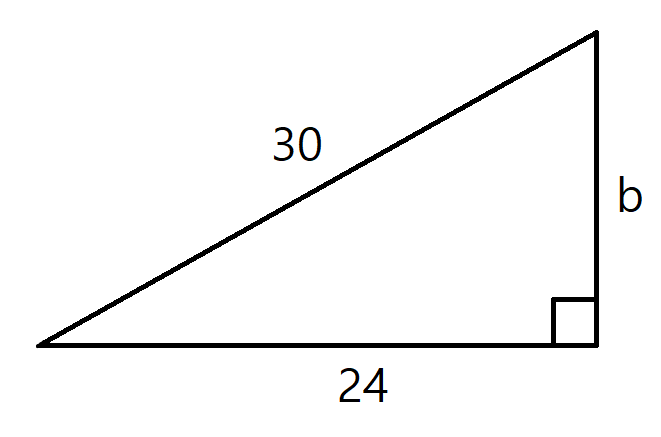
$a^2 + b^2 = c^2$
$24^2 + b^2 = 30^2$
$576 + b^2 = 900$
$b^2 = 900 - 576$
$b = \sqrt{324}$
$b = 18$
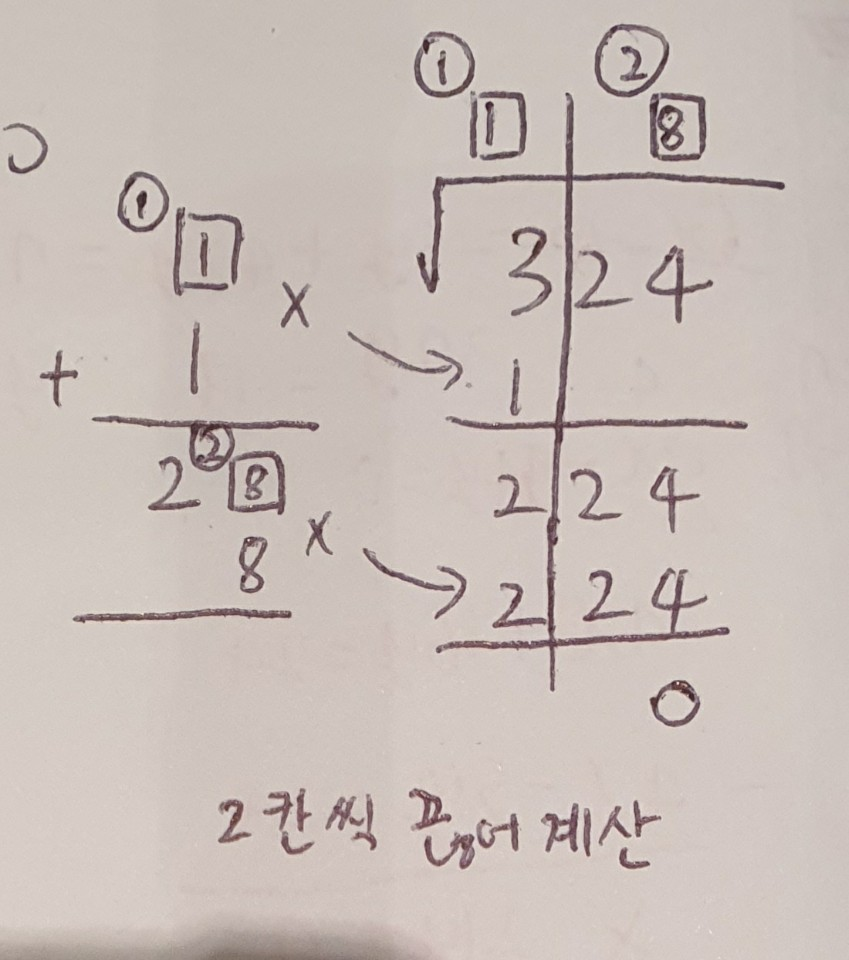
* 더미 지식 : 루트 빠른 계산법
$\sqrt{324} = $
2. 한 삼각형이 세 꼭지점 (30, 75), (25, 0), (-50, 45)로 정의될 때, 이 삼각형은 직각삼각형입니까?
직각삼각형은 피타고라스의 정리인 $A^2 + B^2 = C^2$가 성립되면 된다.
$1. \sqrt{(30 - 25)^2 + (75 - 0)^2} = \sqrt{25 + 5625} = \sqrt{5650}$
$2. \sqrt{(25 - (-50))^2 + (0 - 45)^2} = \sqrt{5625 + 2025} = \sqrt{7650}$
$3. \sqrt{(30 - (-50))^2 + (45 - 75)^2} = \sqrt{6400 + 900} = \sqrt{7300}$
$\sqrt{5650} + \sqrt{7650} != \sqrt{7300}$
정답은 직각삼각형이 아니다.
3. 두점 (30, 80), (150, 130) 사이의 거리를 구하십시오.
$ \sqrt{(150 - 30)^2 + (130 - 80)^2} $
$= \sqrt{14400 + 2500}$
$= 130$
4. 두 점 (20, 50, 10), (100, 120, 40) 사이의 거리를 구하십시오.
$ \sqrt{(100 - 20)^2 + (120 - 50)^2 + (40 - 10)^2} $
$= \sqrt{6400 + 4900 + 900}$
$= 110.45...$
5. 두 점 (30, 80), (150, 130) 사이의 중점을 구하십시오.
$ ((30 + 150)/2, (80 + 130)/2) $
$= (180/2, 210/2)$
$= (90, 105)$
6. 두점 (20, 50, 10), (100, 120, 40) 사이의 중점을 구하십시오.
$ ((20 + 100)/2, (50 + 120)/2, (10 + 40)/2) $
$= (120/2, 170/2, 50/2)$
$= (60, 85, 25)$
'수학 > 게임수학' 카테고리의 다른 글
| [게임수학] 2장 기하학적 기초 - 원과 구 (0) | 2020.06.09 |
|---|---|
| [게임수학] 2장 기하학적 기초 - 포물선 (0) | 2020.05.31 |
| [게임수학] 1장 점과 직선 - 공식 및 핵심요약 (0) | 2020.05.12 |
| [게임수학] 1장 점과 직선 - 충돌 검출 (일차 연립방정식, 선형결합법, 치환법 등) (0) | 2020.05.10 |
| [게임수학] 1장 점과 직선 - 점을 정의하는법 (0) | 2020.05.08 |
- Total
- Today
- Yesterday
- 인터럽트
- 구조
- 포인터
- 메모리
- 게임수학
- c++
- 상속
- 클래스
- 수학
- const
- 초기화
- 입출력
- 함수
- 컴파일
- thread
- 스레드
- 레지스터
- 크기
- New
- dynamic_cast
- 프로세스
- CPU
- 할당
- 백준
- static_cast
- malloc
- 명령어
- 알고리즘
- 멀티스레드
- 운영체제
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |

