티스토리 뷰
피보나치 함수
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
| 0.25 초 (추가 시간 없음) | 128 MB | 203770 | 61802 | 48701 | 32.765% |
문제
다음 소스는 N번째 피보나치 수를 구하는 C++ 함수이다.
int fibonacci(int n) {
if (n == 0) {
printf("0");
return 0;
} else if (n == 1) {
printf("1");
return 1;
} else {
return fibonacci(n‐1) + fibonacci(n‐2);
}
}
fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
- 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
- fibonacci(0)은 0을 출력하고, 0을 리턴한다.
- fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
- 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.
출력
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
예제 입력 1 복사
3
0
1
3
예제 출력 1 복사
1 0
0 1
1 2
예제 입력 2 복사
2
6
22
예제 출력 2 복사
5 8
10946 17711후기
이번 문제는 메모리 제한과 시간 제한을 가장 중요하게 생각해야한다. 또한, 입력 값이 40까지인 것도 눈치채야한다.
메모리 제한, 시간 제한 = 함수 호출 최소화
입력 값 40 = 9 자리의 자연수 출력 = int 형을 사용
위 두 조건을 통해 대충 뭘하라는지 눈치챘다면, 다음은 피보나치 수열이 뭔지 알아야한다. (사실 나도 기억 안났다.)
우리의 전능하신 구글님께서 아주 훌륭한 답변을 주셨다.
'피보나치수열'은 앞 두 개의 항목의 합이 다음 항복의 값이 되는 수열
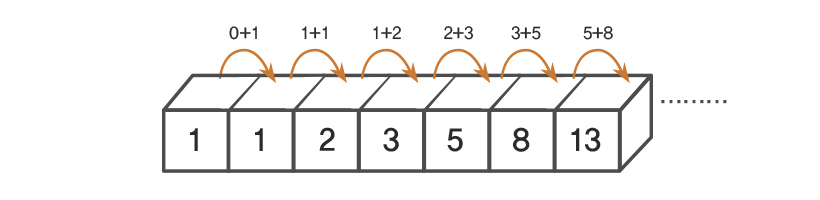
즉, 위와 같이 앞 자리 수 두개가 더해진 값이 피보나치수열에 속하게 되는 것이다.
다른 블러그를 참고하여 다른 그림으로 한번 더 보자.

위 그림들을 통해 $n$이라는 숫자가 주어질 때, $(n-1)+(n-2)=n$이라는 공식이 성립된다.
하지만 문제는 우리에게 피보나치 수열로 만들어지는 0, 1의 개수를 구하라고 한다.
즉, 주어진 숫자 $n$을 0 혹은 1이 나올 때까지 반복하여 $(n-1)$과 $(n-2)$로 분해하라는 것이다.
분명 여기까지만 읽으면 재귀나 반복문을 반복하라는 말 같다. 나도 처음에 그렇게 하다 실패했다.

작성자는 수포자이기에 수식이 들어간 문제들만의 패턴을 알아보고자 종이에 끄적이면서 혼자 생각해봤다.
그러자 나라도 쉽게 알아볼 패턴이 보였는데, 다시 생각해보면 너무나 당연한 것이었다.
$n$을 피보나치수열 방식으로 분해하여 0과 1을 구하는 것이라면 0에서 부터 그냥 피보나치수열로 다시 계산해서 올라가면 되는 것이다.
| 설명 | 입력 값 |
||||||||
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0과 1의 합계 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 0과 1의 낱개 | 0, 1 | 1, 1 | 1, 2 | 2, 3 | 3, 5 | 5, 8 | 8, 13 | 13, 21 | 21, 34 |
위 표를 보면 입력 값에 따른 0과 1의 합계와 각각의 개수를 볼 수 있다.
딱 봐도 합계는 피보나치수열이다. 그런데 0과 1의 낱개가 각 피보나치수열의 직전 $0=(n-2), 1=(n-1)$인 것을 알 수 있다.
즉, 정답은 n의 바로 전 두 개의 수의 0과 1의 합계이다.
$0 = (n - 2)$의 0과 1의 합계 = (n - 2)의 피보나치수열
$1 = (n - 1)$의 0과 1의 합계 = (n - 1)의 피보나치수열
그렇게 작성한 코드는 아래와 같다.
#include <iostream>
using namespace std;
int SearchFibonacci(int n, int *one, int *zero);
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int loop = 0;
cin >> loop;
while (loop--) {
int one = 0;
int zero = 0;
int input = 0;
cin >> input;
if (input > 0) {
SearchFibonacci(input, &one, &zero);
} else {
zero = 1;
}
cout << zero << '\x20' << one << '\n';
}
return 0;
}
int SearchFibonacci(int n, int *one, int *zero) {
(*zero) = 0;
(*one) = 1;
int result = 1;
while (n-- > 1) {
(*zero) = (*one);
(*one) = result;
result = (*zero) + (*one);
}
return result;
}
코드를 보면 피보나치수열 탐색을 1부터 시작하는 것을 알 수 있다. 0은 좀 특수한 경우로 (1, 0)이 반환 되어야 한다.

참고자료
[실습] 피보나치수열
: C 언어 관련 전체 목차 http://blog.naver.com/tipsware/221010831969 1. 피보나치수열 '피...
blog.naver.com
백준 1003 피보나치 함수 개념 및 풀이 (C++)
출처 : https://www.acmicpc.net/problem/1003처음에는 단순히 재귀함수를 사용하여 문제에서 요하는 fibonacci(0), fibonacci(1)의 횟수를 카운트하려고 했다. 하지만 문제의 포인트는 단순히 푸는 것이 아닌 '효
velog.io
'코딩테스트 > BOJ' 카테고리의 다른 글
| [BOJ/C++] 1926::그림 (0) | 2023.11.06 |
|---|---|
| [BOJ/C++] 1004::어린왕자 (0) | 2023.11.05 |
| [BOJ/C++] 2869::달팽이는 올라가고 싶다 (0) | 2023.11.01 |
| [BOJ/C++] 1193::분수찾기 (1) | 2023.10.31 |
| [BOJ/C++] 1158::요세푸스 (Josephus) (1) | 2023.10.31 |
- Total
- Today
- Yesterday
- 메모리
- 백준
- thread
- 멀티스레드
- static_cast
- 클래스
- 운영체제
- 명령어
- New
- 할당
- 입출력
- 상속
- c++
- 프로세스
- 함수
- 컴파일
- 수학
- 포인터
- const
- 알고리즘
- 레지스터
- 스레드
- dynamic_cast
- 크기
- malloc
- CPU
- 구조
- 인터럽트
- 초기화
- 게임수학
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

